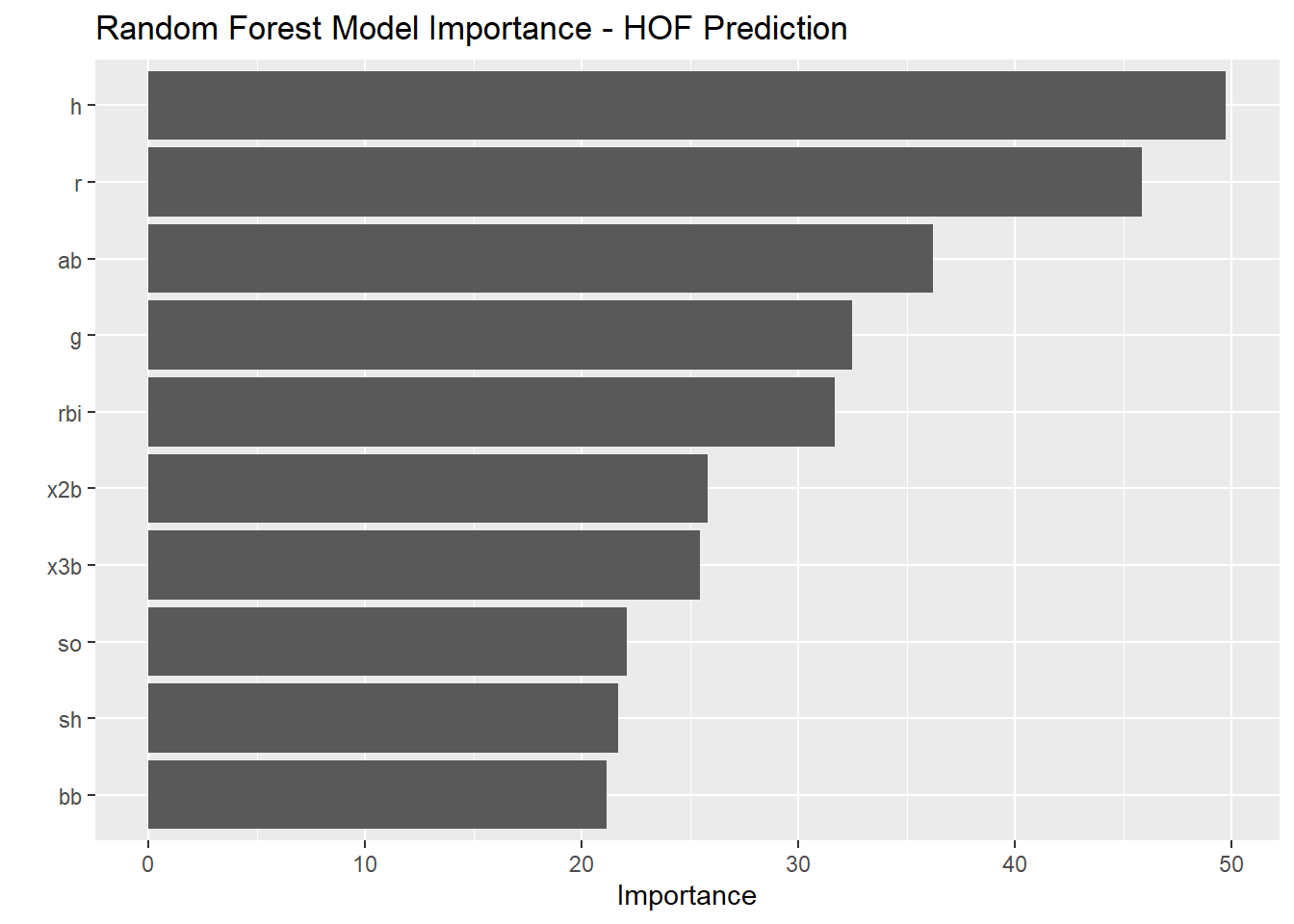
5 Data Modeling

In the last year or so, Max Kuhn, working for RStudio, has developed tidymodels. Tidymodels is a modeling framework that follows tidy coding principles. It provides a streamlined technique for preprocessing, execution, and validation

In this section, you will learn:

A small amount of data exploration.
The basics of tidymodels

splitting data
running multiple models
cross validation
selecting the best model

How to parallelize your code

In this section, we will use the following libraries and data:

library(tidyverse)
library(tidymodels)
library(recipes)
library(tune)
library(janitor)
library(doFuture)
library(yardstick)
library(vip)

data <- read_csv("data_sources/Batting.csv", col_types = cols(SF = col_double(), GIDP = col_double())) %>%
  clean_names()

hofdata <- read_csv("data_sources/HallOfFame.csv")

## Parsed with column specification:
## cols(
##   playerID = col_character(),
##   yearid = col_double(),
##   votedBy = col_character(),
##   ballots = col_double(),
##   needed = col_double(),
##   votes = col_double(),
##   inducted = col_character(),
##   category = col_character(),
##   needed_note = col_character()
## )

head(data)

## # A tibble: 6 x 22
##   player_id year_id stint team_id lg_id     g    ab     r     h   x2b   x3b    hr   rbi    sb    cs    bb    so   ibb   hbp    sh    sf  gidp
##   <chr>       <dbl> <dbl> <chr>   <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 abercda01    1871     1 TRO     <NA>      1     4     0     0     0     0     0     0     0     0     0     0    NA    NA    NA    NA    NA
## 2 addybo01     1871     1 RC1     <NA>     25   118    30    32     6     0     0    13     8     1     4     0    NA    NA    NA    NA    NA
## 3 allisar01    1871     1 CL1     <NA>     29   137    28    40     4     5     0    19     3     1     2     5    NA    NA    NA    NA    NA
## 4 allisdo01    1871     1 WS3     <NA>     27   133    28    44    10     2     2    27     1     1     0     2    NA    NA    NA    NA    NA
## 5 ansonca01    1871     1 RC1     <NA>     25   120    29    39    11     3     0    16     6     2     2     1    NA    NA    NA    NA    NA
## 6 armstbo01    1871     1 FW1     <NA>     12    49     9    11     2     1     0     5     0     1     0     1    NA    NA    NA    NA    NA

head(hofdata)

## # A tibble: 6 x 9
##   playerID  yearid votedBy ballots needed votes inducted category needed_note
##   <chr>      <dbl> <chr>     <dbl>  <dbl> <dbl> <chr>    <chr>    <chr>      
## 1 cobbty01    1936 BBWAA       226    170   222 Y        Player   <NA>       
## 2 ruthba01    1936 BBWAA       226    170   215 Y        Player   <NA>       
## 3 wagneho01   1936 BBWAA       226    170   215 Y        Player   <NA>       
## 4 mathech01   1936 BBWAA       226    170   205 Y        Player   <NA>       
## 5 johnswa01   1936 BBWAA       226    170   189 Y        Player   <NA>       
## 6 lajoina01   1936 BBWAA       226    170   146 N        Player   <NA>

Lets try to develop an informed answer to the question: What baseball statistics help indicate whether or not a baseball player will make the Hall of Fame?

5.1 Prepare Data For Analysis

For this analysis, lets organize our data to identify players who are in the hall of fame as well as those eligible.

hofdata <-
  hofdata %>% 
  clean_names() %>% 
  select(player_id, inducted) %>% 
  mutate(hof = ifelse(inducted=="Y",1,0)) %>% 
  filter(hof==1)

hofdata %>%  count(inducted)

## # A tibble: 1 x 2
##   inducted     n
##   <chr>    <int>
## 1 Y          317

years_played <- 
data %>% 
  group_by(player_id) %>% 
  summarise(across(year_id, .fns = c("min" = min, "max" = max))) %>%  # dplyr 1.0.0
  mutate(total_years = year_id_max - year_id_min)

## `summarise()` ungrouping output (override with `.groups` argument)

years_played

## # A tibble: 18,915 x 4
##    player_id year_id_min year_id_max total_years
##    <chr>           <dbl>       <dbl>       <dbl>
##  1 aardsda01        2004        2015          11
##  2 aaronha01        1954        1976          22
##  3 aaronto01        1962        1971           9
##  4 aasedo01         1977        1990          13
##  5 abadan01         2001        2006           5
##  6 abadfe01         2010        2016           6
##  7 abadijo01        1875        1875           0
##  8 abbated01        1897        1910          13
##  9 abbeybe01        1892        1896           4
## 10 abbeych01        1893        1897           4
## # ... with 18,905 more rows

hof <-
  data %>% 
  group_by(player_id) %>% 
  summarise_at(vars(g:gidp), list(~sum(.,na.rm = TRUE))) %>%
  ungroup() %>%  
  left_join(years_played, by = "player_id") %>% 
  left_join(hofdata, by = "player_id") %>% 
  mutate(inducted = if_else(inducted=="Y",1,0)) %>% 
  mutate(inducted = replace_na(inducted, 0)) %>% 
  filter(total_years >= 10) %>% 
  # filter(g>=1000) %>% 
  mutate(inducted = as.factor(inducted)) %>% 
  select(-hof)

hof

## # A tibble: 3,475 x 22
##    player_id     g    ab     r     h   x2b   x3b    hr   rbi    sb    cs    bb    so   ibb   hbp    sh    sf  gidp year_id_min year_id_max total_years inducted
##    <chr>     <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>       <dbl>       <dbl>       <dbl> <fct>   
##  1 aardsda01   331     4     0     0     0     0     0     0     0     0     0     2     0     0     1     0     0        2004        2015          11 0       
##  2 aaronha01  3298 12364  2174  3771   624    98   755  2297   240    73  1402  1383   293    32    21   121   328        1954        1976          22 1       
##  3 aasedo01    448     5     0     0     0     0     0     0     0     0     0     3     0     0     0     0     0        1977        1990          13 0       
##  4 abbated01   855  3044   355   772    99    43    11   324   142     0   289    16     0    33    93     0     0        1897        1910          13 0       
##  5 abbotgl01   248     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0        1973        1984          11 0       
##  6 abbotji01   263    21     0     2     0     0     0     3     0     0     0    10     0     0     3     0     1        1989        1999          10 0       
##  7 abbotpa01   162    20     2     5     1     0     0     2     0     0     0     6     0     0     5     0     0        1990        2004          14 0       
##  8 abernte02   681   181    12    25     3     0     0     9     0     0     6    74     0     2    15     0     4        1955        1972          17 0       
##  9 abreubo01  2425  8480  1453  2470   574    59   288  1363   400   128  1476  1840   115    33     7    85   165        1996        2014          18 0       
## 10 adairje01  1165  4019   378  1022   163    19    57   366    29    29   208   499    31    17    41    30   149        1958        1970          12 0       
## # ... with 3,465 more rows

Filter for HOF Eligible Players

hof %>% 
  filter(year_id_max <= 2012) %>% 
  count(inducted)

## # A tibble: 2 x 2
##   inducted     n
##   <fct>    <int>
## 1 0         2921
## 2 1          232

hofmod <-
hof %>% 
  filter(year_id_max <= 2012) %>% 
  select(-contains("year"))
hofmod

## # A tibble: 3,153 x 19
##    player_id     g    ab     r     h   x2b   x3b    hr   rbi    sb    cs    bb    so   ibb   hbp    sh    sf  gidp inducted
##    <chr>     <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <fct>   
##  1 aaronha01  3298 12364  2174  3771   624    98   755  2297   240    73  1402  1383   293    32    21   121   328 1       
##  2 aasedo01    448     5     0     0     0     0     0     0     0     0     0     3     0     0     0     0     0 0       
##  3 abbated01   855  3044   355   772    99    43    11   324   142     0   289    16     0    33    93     0     0 0       
##  4 abbotgl01   248     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0 0       
##  5 abbotji01   263    21     0     2     0     0     0     3     0     0     0    10     0     0     3     0     1 0       
##  6 abbotpa01   162    20     2     5     1     0     0     2     0     0     0     6     0     0     5     0     0 0       
##  7 abernte02   681   181    12    25     3     0     0     9     0     0     6    74     0     2    15     0     4 0       
##  8 adairje01  1165  4019   378  1022   163    19    57   366    29    29   208   499    31    17    41    30   149 0       
##  9 adamsba01   482  1019    79   216    31    15     3    75     1     1    53   177     0     1    35     0     0 0       
## 10 adamsbo03  1281  4019   591  1082   188    49    37   303    67    30   414   447     1    17    78     5    62 0       
## # ... with 3,143 more rows

hoftest <-
hof %>% 
  filter(year_id_max > 2012) %>% 
  select(-contains("year"),-inducted)
hoftest

## # A tibble: 322 x 18
##    player_id     g    ab     r     h   x2b   x3b    hr   rbi    sb    cs    bb    so   ibb   hbp    sh    sf  gidp
##    <chr>     <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
##  1 aardsda01   331     4     0     0     0     0     0     0     0     0     0     2     0     0     1     0     0
##  2 abreubo01  2425  8480  1453  2470   574    59   288  1363   400   128  1476  1840   115    33     7    85   165
##  3 adamsmi03   410     2     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
##  4 affelje01   774    17     0     3     0     0     0     2     0     0     2     6     0     0     0     0     0
##  5 alberma01   452    35     1     3     1     0     0     0     0     0     0    21     0     0     3     0     0
##  6 andinro01   481  1344   159   313    58     1    18    97    24    12   113   313     2     6    21     7    42
##  7 ankieri01   653  1921   260   462   101    10    76   251    21    12   162   555    13    12     8    12    31
##  8 arroybr01   421   603    35    77    16     0     6    29     1     0    14   266     0     1    82     3     8
##  9 atchisc01   300     2     0     0     0     0     0     0     0     0     0     1     0     0     0     0     0
## 10 ayalalu01   534    14     0     4     1     0     0     0     0     0     0     3     0     0     3     0     0
## # ... with 312 more rows

5.2 Data Exploration

Percentage of players in the dataset who are in the HOF

hofmod %>% count(inducted) %>% mutate(prop = n/sum(n))

## # A tibble: 2 x 3
##   inducted     n   prop
##   <fct>    <int>  <dbl>
## 1 0         2921 0.926 
## 2 1          232 0.0736

Visual difference in statistics between HOF and non HOF

hof %>% 
  select(g:gidp, inducted) %>%  
  pivot_longer(cols = g:gidp) %>% 
  group_by(inducted,name) %>% 
  summarise(
    lwr_quantile = quantile(value, c(.025)),
    median = quantile(value, c(.5)),
    upper_quantile = quantile(value, c(.975)),
            ) %>% 
  ggplot(aes(x=inducted,y=median)) +
  geom_point() +
  geom_errorbar(aes(ymin = lwr_quantile, ymax = upper_quantile)) +
  theme(legend.position = "none") +
  labs(x= "",y = "", title = "Differences Between HOF and non-HOF") +
  facet_wrap(~name, scales = "free")

## `summarise()` regrouping output by 'inducted' (override with `.groups` argument)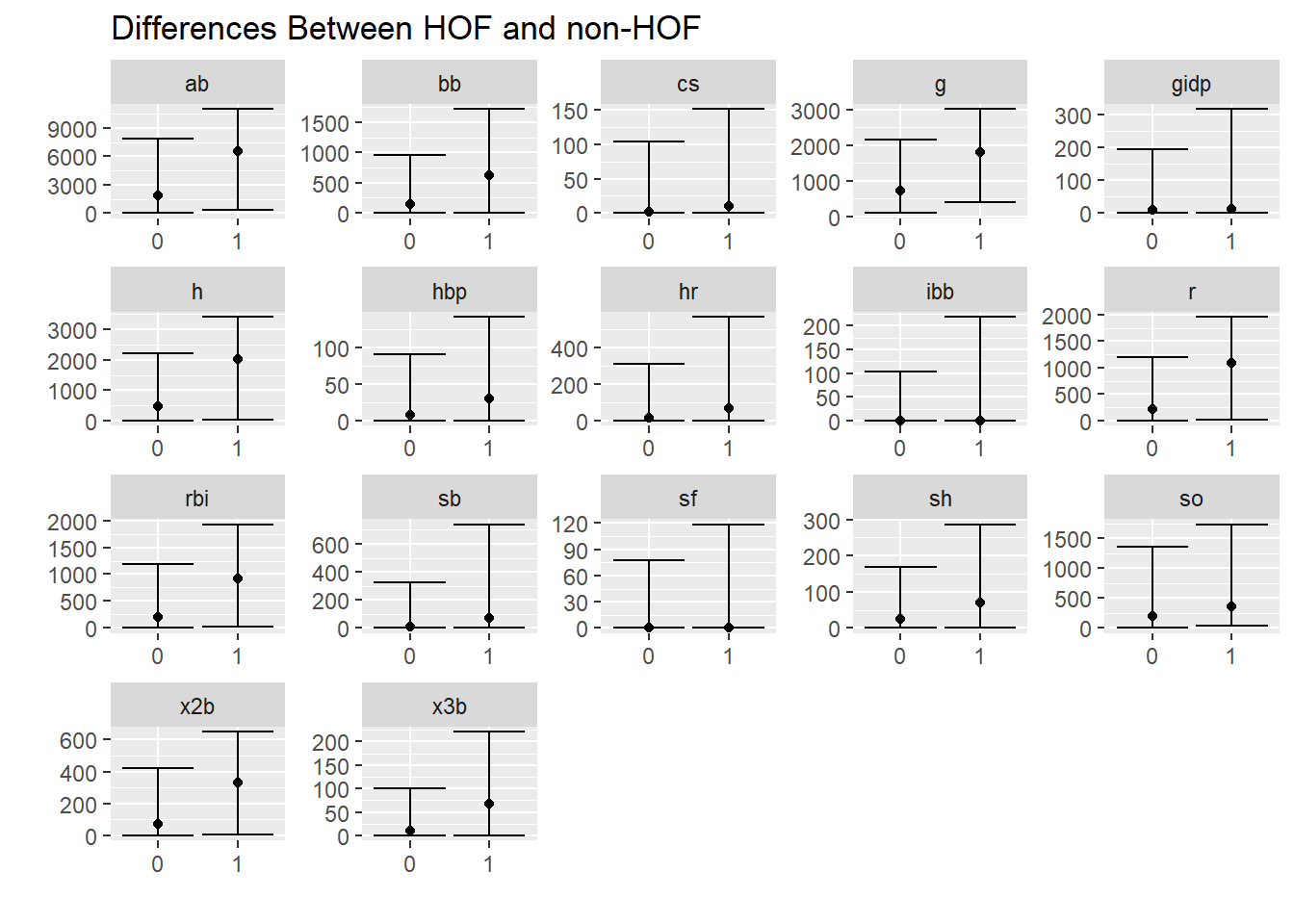

Well, won’t players who are in the HOF had played longer? Therefore they should have more hits, home runs, etc?

Lets compare the number of games of players in the HOF vs out of the HOF.

hof %>% 
  select(g, inducted) %>%  
  ggplot(aes(x=g, fill = inducted)) +
  geom_density() +
  labs(x="Games", y = "", fill = "HOF",
       title = "Density of Game / HOF Stats")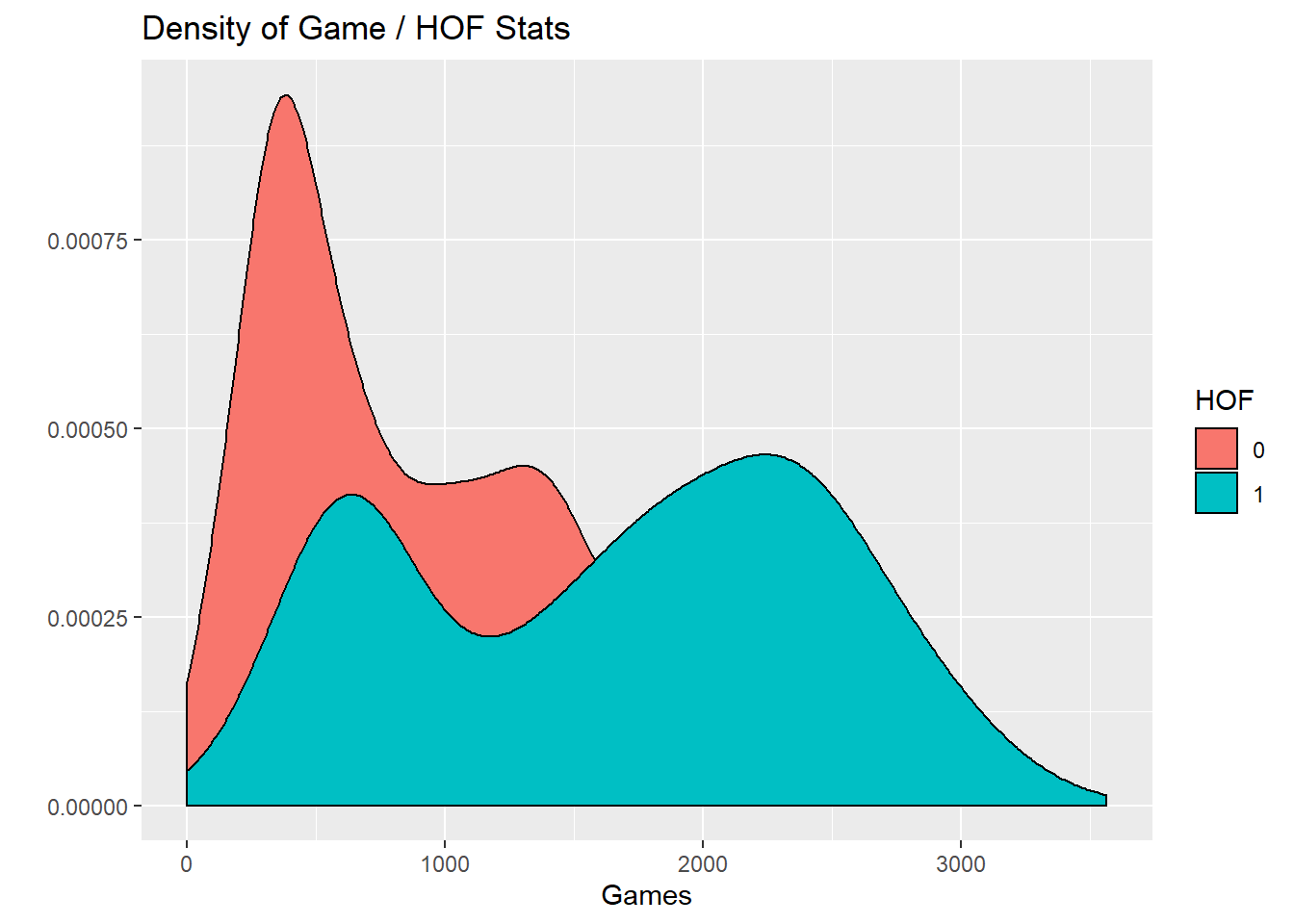

Lets look at this for every statistic

hof %>% 
  select(g:gidp, inducted) %>%  
  pivot_longer(cols = g:gidp) %>% 
  ggplot(aes(x=value, fill = inducted)) +
  geom_density() +
  facet_wrap(~name, scales = "free") +
  labs(x="",y = "", fill = "HOF",
       title = "Density of Stats for Players In/Out of HOF")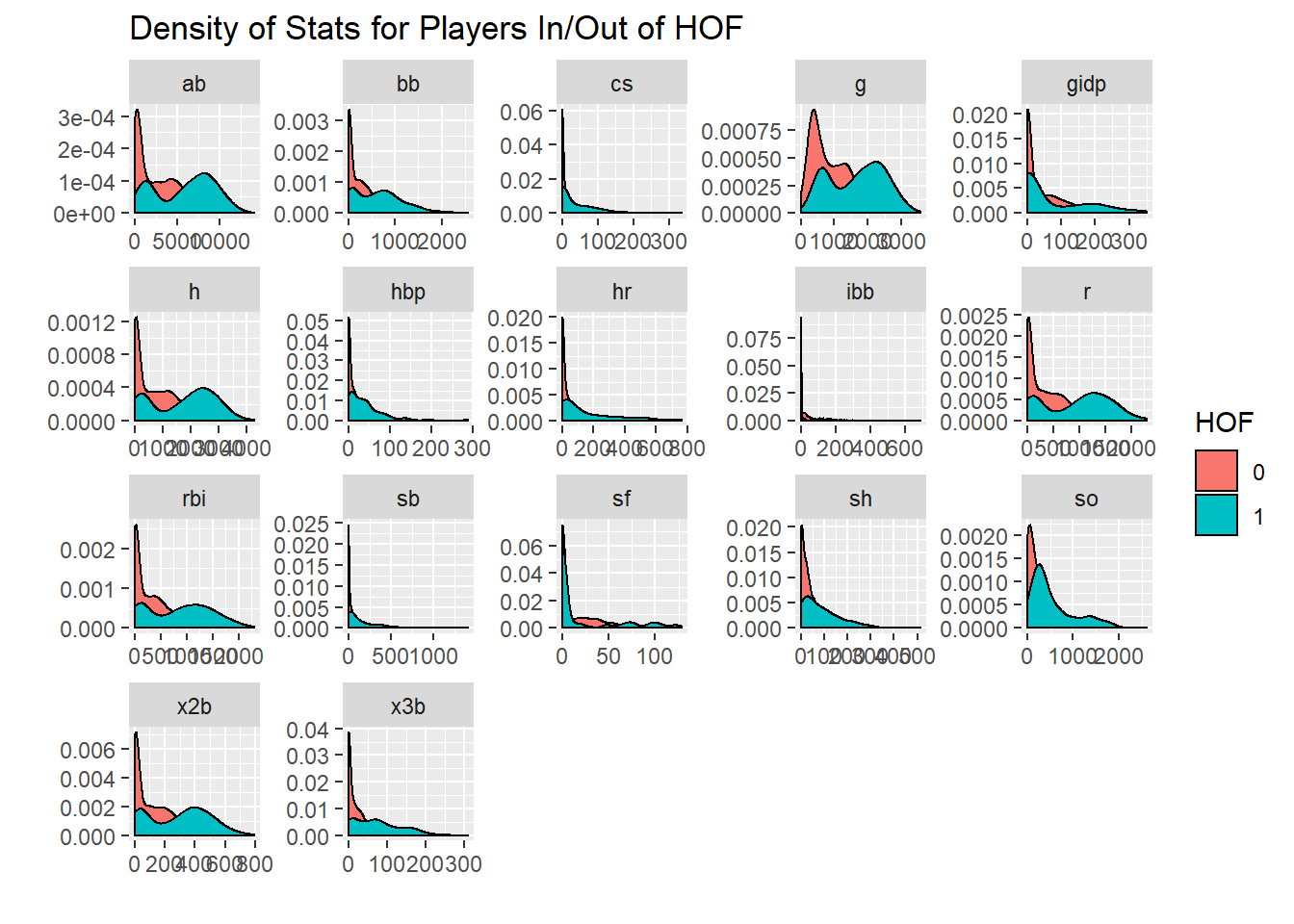

5.3 Split Data test/train

To begin modeling, we’ll need to split our data into a testing, training, and validation set.

set.seed(str_length("beatnavy"))
hof_initial_split <- initial_split(hofmod, prop = 0.80)
hof_initial_split

## <2523/630/3153>

5.4 Preprocess Data

A recipe is a description of what steps should be applied to a data set in order to get it ready for data analysis.

tidymodels / recipes currently offers about 30 ‘steps’. More documentation for the recipes package is here

We first specify the “recipe” or specify what we are trying to model and with what data.

recipe(inducted ~ ., data = training(hof_initial_split))

## Data Recipe
## 
## Inputs:
## 
##       role #variables
##    outcome          1
##  predictor         18

From here, we need to specify other preprocessing steps. We will add these to the recipe.

Once we complete these steps, we ‘prep’ the data.

preprocessing_recipe <-
  recipe(inducted ~ ., data = training(hof_initial_split)) %>%
  step_knnimpute(all_numeric()) %>% 
  step_center(all_numeric()) %>% 
  step_scale(all_numeric()) %>% 
  step_rm(player_id) %>%
  prep()
preprocessing_recipe

## Data Recipe
## 
## Inputs:
## 
##       role #variables
##    outcome          1
##  predictor         18
## 
## Training data contained 2523 data points and no missing data.
## 
## Operations:
## 
## K-nearest neighbor imputation for player_id, ab, r, h, x2b, x3b, hr, rbi, sb, cs, bb, so, ibb, hbp, sh, sf, gidp, g [trained]
## Centering for g, ab, r, h, x2b, x3b, hr, rbi, sb, cs, bb, so, ibb, hbp, sh, sf, gidp [trained]
## Scaling for g, ab, r, h, x2b, x3b, hr, rbi, sb, cs, bb, so, ibb, hbp, sh, sf, gidp [trained]
## Variables removed player_id [trained]

5.5 Apply Preprocessing

For a recipe with at least one preprocessing operations that has been trained by recipe(), apply the computations to the data.

hof_training_preprocessed_tbl <- 
  preprocessing_recipe %>% 
  bake(training(hof_initial_split))

hof_training_preprocessed_tbl

## # A tibble: 2,523 x 18
##         g     ab       r      h    x2b    x3b      hr     rbi      sb     cs     bb     so    ibb     hbp      sh     sf   gidp inducted
##     <dbl>  <dbl>   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>   <dbl>   <dbl>  <dbl>  <dbl>  <dbl>  <dbl>   <dbl>   <dbl>  <dbl>  <dbl> <fct>   
##  1  3.72   3.65   4.29    3.95   3.62   1.99   7.24    4.97    1.69    1.70   3.55   2.83   7.85   0.439  -0.415   4.56   4.65  1       
##  2 -0.770 -1.06  -0.919  -0.980 -0.926 -0.747 -0.606  -0.891  -0.550  -0.619 -0.847 -0.911 -0.444 -0.673  -0.820  -0.590 -0.714 0       
##  3 -1.09  -1.06  -0.919  -0.980 -0.926 -0.747 -0.606  -0.891  -0.550  -0.619 -0.847 -0.920 -0.444 -0.673  -0.820  -0.590 -0.714 0       
##  4 -1.06  -1.05  -0.919  -0.977 -0.926 -0.747 -0.606  -0.884  -0.550  -0.619 -0.847 -0.892 -0.444 -0.673  -0.762  -0.590 -0.697 0       
##  5 -1.22  -1.05  -0.914  -0.973 -0.919 -0.747 -0.606  -0.886  -0.550  -0.619 -0.847 -0.903 -0.444 -0.673  -0.724  -0.590 -0.714 0       
##  6 -0.403 -0.993 -0.890  -0.947 -0.904 -0.747 -0.606  -0.868  -0.550  -0.619 -0.828 -0.719 -0.444 -0.604  -0.531  -0.590 -0.648 0       
##  7  0.360  0.470 -0.0125  0.355  0.262 -0.215 -0.0132  0.0431 -0.279   0.301 -0.195  0.432  0.433 -0.0824 -0.0299  0.688  1.72  0       
##  8 -0.717 -0.674 -0.730  -0.698 -0.700 -0.327 -0.574  -0.700  -0.540  -0.587 -0.681 -0.440 -0.444 -0.638  -0.146  -0.590 -0.714 0       
##  9  0.543  0.470  0.498   0.433  0.444  0.624 -0.221  -0.118   0.0751  0.332  0.452  0.292 -0.416 -0.0824  0.683  -0.377  0.301 0       
## 10  0.768  1.06   1.11    1.09   0.889  0.596 -0.512   0.115   0.886   0.967  0.574 -0.315 -0.444  0.300   1.80   -0.590 -0.485 0       
## # ... with 2,513 more rows

5.6 Prepare Cross Validation

This partitions our data into v folds. In our case, 5.

This yields a data frame with a nested list of training / testing data.

set.seed(str_length("beatnavy"))
hof_cv_folds <-
  training(hof_initial_split) %>% 
    bake(preprocessing_recipe, new_data = .) %>%
    vfold_cv(v = 5)
hof_cv_folds

## #  5-fold cross-validation 
## # A tibble: 5 x 2
##   splits           id   
##   <named list>     <chr>
## 1 <split [2K/505]> Fold1
## 2 <split [2K/505]> Fold2
## 3 <split [2K/505]> Fold3
## 4 <split [2K/504]> Fold4
## 5 <split [2K/504]> Fold5

5.7 Specify Models

Now that we’ve prepared our data, we must specify the models which want to compare. We’ll look at 2.

You must first specify the model type (logistic_reg() and rand_forest in the examples below). There are many to choose from in the parsnip package. Documentation can be found here.

The motivation behind this package from the documentation, "Modeling functions across different R packages can have very different interfaces. If you would like to try different approaches, there is a lot of syntactical minutiae to remember. The problem worsens when you move in-between platforms.

“parsnip tries to solve this by providing similar interfaces to models. For example, if you are fitting a random forest model and would like to adjust the number of trees in the forest there are different argument names to remember depending on the random forest package you chose…” (such as rf or randomforest).

After you specify the model type, you can provide

GLM Model

glmnet_model <-
  logistic_reg(mode = "classification",
    penalty = tune(),
    mixture = tune()) %>%
  set_engine("glmnet")

glmnet_model

## Logistic Regression Model Specification (classification)
## 
## Main Arguments:
##   penalty = tune()
##   mixture = tune()
## 
## Computational engine: glmnet

Random Forest Model

Notice how in the previous model and in this model, I specified several tuning parameters. Other than penalty, and mixture, there are many to chose from. These include mode, mtry, trees, and min_n among others.. I can specify these values, but I have chose to ‘tune’ them through cross validation in later steps.

forest_model <-
  rand_forest(
    mode = "classification",
    mtry = tune(),
    trees = tune(),
    min_n = tune()
  ) %>%
  set_engine("randomForest", objective = "reg:squarederror")

forest_model

## Random Forest Model Specification (classification)
## 
## Main Arguments:
##   mtry = tune()
##   trees = tune()
##   min_n = tune()
## 
## Engine-Specific Arguments:
##   objective = reg:squarederror
## 
## Computational engine: randomForest

5.8 Create Grid of Parameters to Validate Over

Here we specify the tuning parameters for cross validation and take a look visually at the parameter space we are covering in efforts to reach the best model.

GLM Model

glmnet_params <- parameters(penalty(), mixture())
glmnet_params

## Collection of 2 parameters for tuning
## 
##       id parameter type object class
##  penalty        penalty    nparam[+]
##  mixture        mixture    nparam[+]

set.seed(str_length("beatnavy"))
glmnet_grid = grid_max_entropy(glmnet_params, size = 20)
glmnet_grid

## # A tibble: 20 x 2
##     penalty mixture
##       <dbl>   <dbl>
##  1 6.31e- 9  0.558 
##  2 3.73e- 4  0.368 
##  3 2.05e- 9  0.805 
##  4 1.71e-10  0.0903
##  5 6.00e- 1  0.620 
##  6 2.15e- 8  0.195 
##  7 1.72e- 2  0.850 
##  8 1.78e-10  0.317 
##  9 8.94e- 4  0.947 
## 10 5.45e- 7  0.809 
## 11 3.69e- 5  0.0202
## 12 3.71e- 2  0.0778
## 13 3.01e- 7  0.993 
## 14 2.49e- 4  0.703 
## 15 2.49e- 8  0.0277
## 16 9.08e- 7  0.532 
## 17 3.13e- 1  0.344 
## 18 3.80e-10  0.671 
## 19 6.00e- 7  0.294 
## 20 4.37e- 4  0.176

glmnet_grid %>%
  ggplot(aes(penalty, mixture)) +
  geom_point(size = 3) +
  scale_x_log10() +
  labs(title = "Max Entropy Grid", x = "Penalty (log scale)", y = "Mixture")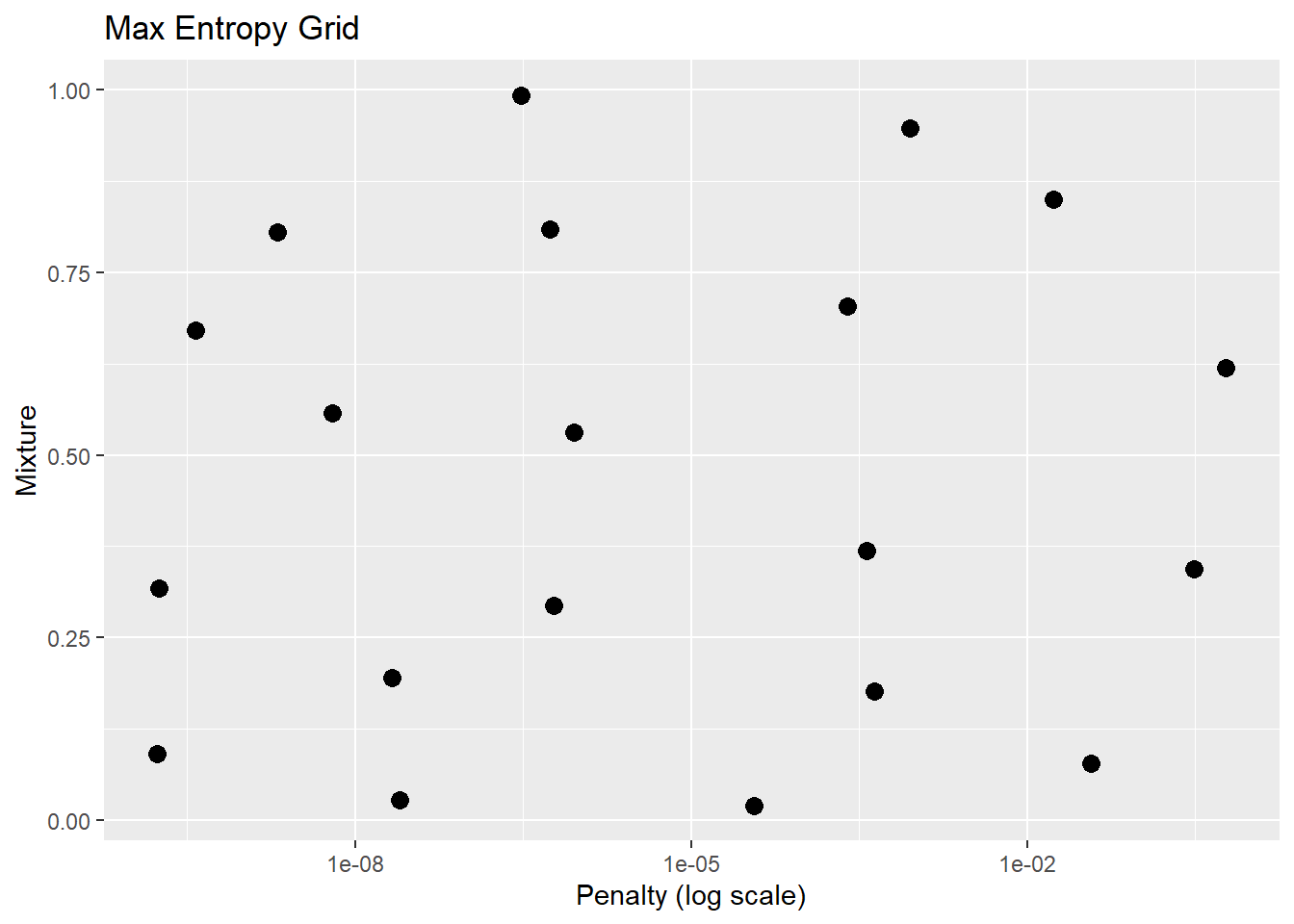

Random Forest Model

forest_params <- parameters(mtry(c(2,6)), trees(), min_n())
forest_params

## Collection of 3 parameters for tuning
## 
##     id parameter type object class
##   mtry           mtry    nparam[+]
##  trees          trees    nparam[+]
##  min_n          min_n    nparam[+]

set.seed(str_length("beatnavy"))
forest_grid <- grid_max_entropy(forest_params, size = 30)
forest_grid

## # A tibble: 30 x 3
##     mtry trees min_n
##    <int> <int> <int>
##  1     3  1714     5
##  2     4   368    28
##  3     3  1607    39
##  4     3  1207    14
##  5     5    42    37
##  6     4   892    27
##  7     3  1154    25
##  8     5  1678     2
##  9     4   607    10
## 10     3   803    37
## # ... with 20 more rows

5.9 Execute Cross Validation

5.9.1 Parallel Processing

The great thing about cross validation is that tunes parameters to find the model which performs the best on the out-of-sample test data.

The problem is that this can be computationally intensive.

Thankfully tidymodels is capable of running over multiple cores. You can see from the code below my computer has 4 cores. Your mileage may vary.

all_cores <- parallel::detectCores(logical = FALSE)
all_cores

## [1] 4

registerDoFuture()
cl <- makeCluster(all_cores)
plan(cluster, workers = cl)

GLM Model

The code below kicks off the cross validation of your model. You can see the time it takes to run the code over multiple cores

tictoc::tic()
glmnet_stage_1_cv_results_tbl <- tune_grid(
          object = glmnet_model, 
          inducted ~ ., 
          resamples = hof_cv_folds, 
          grid = glmnet_grid, 
          # grid = forest_grid, 
          metrics = metric_set(accuracy, kap, roc_auc), 
          control = control_grid(verbose = TRUE)
          )
tictoc::toc()

## 37.58 sec elapsed

The output of the cross validation is a tibble with nested columns. Of note, in the columns are the data and the performance.

glmnet_stage_1_cv_results_tbl

## #  5-fold cross-validation 
## # A tibble: 5 x 4
##   splits           id    .metrics          .notes          
## * <named list>     <chr> <list>            <list>          
## 1 <split [2K/505]> Fold1 <tibble [60 x 5]> <tibble [0 x 1]>
## 2 <split [2K/505]> Fold2 <tibble [60 x 5]> <tibble [0 x 1]>
## 3 <split [2K/505]> Fold3 <tibble [60 x 5]> <tibble [0 x 1]>
## 4 <split [2K/504]> Fold4 <tibble [60 x 5]> <tibble [0 x 1]>
## 5 <split [2K/504]> Fold5 <tibble [60 x 5]> <tibble [0 x 1]>

We can manipulate the dataframe to extract the data we need, however, the tune package provides a function to help us out.

glmnet_stage_1_cv_results_tbl %>% show_best("accuracy", n = 5) %>% bind_rows(
glmnet_stage_1_cv_results_tbl %>% show_best("kap", n = 5)) %>% bind_rows(
glmnet_stage_1_cv_results_tbl %>% show_best("roc_auc", n = 5))

## # A tibble: 15 x 7
##     penalty mixture .metric  .estimator  mean     n std_err
##       <dbl>   <dbl> <chr>    <chr>      <dbl> <int>   <dbl>
##  1 2.05e- 9   0.805 accuracy binary     0.935     5 0.00361
##  2 6.31e- 9   0.558 accuracy binary     0.935     5 0.00361
##  3 5.45e- 7   0.809 accuracy binary     0.935     5 0.00361
##  4 9.08e- 7   0.532 accuracy binary     0.935     5 0.00361
##  5 3.80e-10   0.671 accuracy binary     0.935     5 0.00348
##  6 2.05e- 9   0.805 kap      binary     0.378     5 0.0273 
##  7 6.31e- 9   0.558 kap      binary     0.378     5 0.0273 
##  8 5.45e- 7   0.809 kap      binary     0.378     5 0.0273 
##  9 9.08e- 7   0.532 kap      binary     0.378     5 0.0273 
## 10 3.80e-10   0.671 kap      binary     0.376     5 0.0264 
## 11 6.31e- 9   0.558 roc_auc  binary     0.837     5 0.0168 
## 12 9.08e- 7   0.532 roc_auc  binary     0.837     5 0.0168 
## 13 3.80e-10   0.671 roc_auc  binary     0.837     5 0.0169 
## 14 6.00e- 7   0.294 roc_auc  binary     0.836     5 0.0168 
## 15 1.78e-10   0.317 roc_auc  binary     0.836     5 0.0168

Random Forest Model

This following code took quite a bit of time - but would have taken about 5 times as long if not parallelized.

Since we explained the code above, we will not break up this code below.

tictoc::tic()
forest_stage_1_cv_results_tbl <- tune_grid(
    formula   = inducted ~ .,
    model     = forest_model,
    resamples = hof_cv_folds,
    grid      = forest_grid,
    metrics   = metric_set(accuracy, kap, roc_auc),
    control   = control_grid(verbose = TRUE)
)
tictoc::toc()

## 153.64 sec elapsed

forest_stage_1_cv_results_tbl

## #  5-fold cross-validation 
## # A tibble: 5 x 4
##   splits           id    .metrics          .notes          
## * <named list>     <chr> <list>            <list>          
## 1 <split [2K/505]> Fold1 <tibble [90 x 6]> <tibble [0 x 1]>
## 2 <split [2K/505]> Fold2 <tibble [90 x 6]> <tibble [0 x 1]>
## 3 <split [2K/505]> Fold3 <tibble [90 x 6]> <tibble [0 x 1]>
## 4 <split [2K/504]> Fold4 <tibble [90 x 6]> <tibble [0 x 1]>
## 5 <split [2K/504]> Fold5 <tibble [90 x 6]> <tibble [0 x 1]>

forest_stage_1_cv_results_tbl %>% show_best("accuracy", n = 5) %>% bind_rows(
forest_stage_1_cv_results_tbl %>% show_best("kap", n = 5)) %>% bind_rows(
forest_stage_1_cv_results_tbl %>% show_best("roc_auc", n = 5))

## # A tibble: 15 x 8
##     mtry trees min_n .metric  .estimator  mean     n std_err
##    <int> <int> <int> <chr>    <chr>      <dbl> <int>   <dbl>
##  1     6  1096    13 accuracy binary     0.944     5 0.00417
##  2     3   985    11 accuracy binary     0.944     5 0.00467
##  3     5  1678     2 accuracy binary     0.944     5 0.00310
##  4     3  1714     5 accuracy binary     0.943     5 0.00445
##  5     5  1753    27 accuracy binary     0.943     5 0.00445
##  6     6  1096    13 kap      binary     0.510     5 0.0262 
##  7     5  1678     2 kap      binary     0.508     5 0.0214 
##  8     3   985    11 kap      binary     0.507     5 0.0294 
##  9     3  1714     5 kap      binary     0.505     5 0.0267 
## 10     5  1974    13 kap      binary     0.504     5 0.0266 
## 11     3   877     3 roc_auc  binary     0.927     5 0.00282
## 12     3  1714     5 roc_auc  binary     0.924     5 0.00193
## 13     4   906    16 roc_auc  binary     0.922     5 0.00275
## 14     4   607    10 roc_auc  binary     0.922     5 0.00148
## 15     4  1942    21 roc_auc  binary     0.922     5 0.00159

5.10 Select Best Parameters

Now that both models are cross validated, we can select the tuning parameters which minimized our error metric.

params_glmnet_best <- 
  glmnet_stage_1_cv_results_tbl %>% 
  select_best("roc_auc")

params_glmnet_best

## # A tibble: 1 x 2
##         penalty mixture
##           <dbl>   <dbl>
## 1 0.00000000631   0.558

params_forest_best <-
  forest_stage_1_cv_results_tbl %>% 
  select_best("roc_auc")

params_forest_best

## # A tibble: 1 x 3
##    mtry trees min_n
##   <int> <int> <int>
## 1     3   877     3

5.11 Execute Models With Best Parameters

glmnet_stage_2_model <-
  glmnet_model %>% 
  finalize_model(parameters = params_glmnet_best)

glmnet_stage_2_model

## Logistic Regression Model Specification (classification)
## 
## Main Arguments:
##   penalty = 6.31006806439131e-09
##   mixture = 0.55818817159161
## 
## Computational engine: glmnet

forest_stage_2_model <-
  forest_model %>% 
  finalize_model(params_forest_best)

forest_stage_2_model

## Random Forest Model Specification (classification)
## 
## Main Arguments:
##   mtry = 3
##   trees = 877
##   min_n = 3
## 
## Engine-Specific Arguments:
##   objective = reg:squarederror
## 
## Computational engine: randomForest

5.12 Compare Models

Now we need to compare the ‘winning’ specifications from our two models to see which one performs best on our error metric.

First we apply our preprocessing recipe to our training and test sets.

train_processed <-
  training(hof_initial_split) %>% 
  bake(preprocessing_recipe, new_data = .)

test_processed <-
  testing(hof_initial_split) %>% 
  bake(preprocessing_recipe, new_data = .)

Next, we are identifying the variable in which we are predicting (inducted in this instance), then using the metrics function from the yardstick library to estimate the performance of each model.

target_expr <-
  preprocessing_recipe %>% 
    pluck("last_term_info") %>%
    filter(role == "outcome") %>%
    pull(variable) %>%
    sym()

glmnet_stage_2_metrics <-
  glmnet_stage_2_model %>%
  fit(formula = inducted ~ ., data = train_processed) %>%
  predict(new_data = test_processed) %>%
  bind_cols(testing(hof_initial_split)) %>%
  metrics(!! target_expr, .pred_class)

forest_stage_2_metrics <-   
  forest_stage_2_model %>%
  fit(formula = inducted ~ ., data = train_processed) %>%
  predict(new_data = test_processed) %>%
  bind_cols(testing(hof_initial_split)) %>%
  metrics(!! target_expr, .pred_class)

Here, we pretty up the code for easy consumption.

glmnet_stage_2_metrics %>% 
  mutate(mod = "glmnet") %>% 
  bind_rows(
    forest_stage_2_metrics %>% 
      mutate(mod = "forest")
    ) %>% 
  arrange(.metric,-.estimate)

## # A tibble: 4 x 4
##   .metric  .estimator .estimate mod   
##   <chr>    <chr>          <dbl> <chr> 
## 1 accuracy binary         0.946 forest
## 2 accuracy binary         0.941 glmnet
## 3 kap      binary         0.425 forest
## 4 kap      binary         0.345 glmnet

Looks like the Random Forest is the better model.

5.13 Run Best Model on All Data

model_final <-forest_stage_2_model %>%
    fit(inducted ~ . , data = bake(preprocessing_recipe, new_data = hofmod))

5.14 Run Model on New Data

5.15 Variable Importance

vip(model_final) +
    labs(title = "Random Forest Model Importance - HOF Prediction")

Many Thanks